Understanding Insertion Sort

Introduction to Insertion Sort

Imagine you are given a hand of playing cards and told to sort them. What sorting algorithm would you use? Odds are, you'd find yourself using insertion sort. Most of us humans have two hands, so it makes sense to us to take one card at a time from our right hand and put it in its sorted place in our left hand. Once all of the cards have been moved from right to left, we have a sorted hand of cards!

What do we need to do?

This task is fairly intuitive for us humans, but to teach a computer how to do it correctly we're going to need to break it down into its component parts. Let's list out all of the little steps we need to perform:

1. Pick a value from the "right hand" (the unsorted section)
2. Locate its proper position in the "left hand" (the sorted section)
3. Insert the value into that position

Step 3 will be the hardest. In our playing cards example, we can just slide our new card in between its two neighbors, but you can't just "slide" a long int in between two others - we're going to need to move some other values out of the way first.

The CLRS Pseudocode

(you can skip this if you don't use the CLRS book)

Here's what our book gives us:

for j <- 2 to length[A]
    do key <- A[j]
        i <- j - 1
        while i > 0 and A[i] > key
            do A[i + 1] <- A[i]
                i <- i - 1
        A[i + 1] = key

Not exactly the most understandable pseudocode, so let's break it down. Most of the pseudocode is actually performing one operation: the combined action of finding out where the new value should go, and moving the other values out of the way (steps 2 and 3 above). We can make it easier to look at:

for j <- 2 to length[A] // for every value in the array
    do key <- A[j] // take the value and call it "key"
        >> find out where key should go,
        >> and move values that are in the way
        A[i + 1] = key // stick key in the right spot

Now, let's work on turning that pseudocode into real code.

The Insertion Step

We've established that the insertion step is the most complex portion of this algorithm. Let's take a swing at it. Basically, we have some values that are already sorted, and we need to insert a new value into its sorted position. To achieve this, we scan the sorted values from right to left, looking for the first element that is equal to or less than the new one. Whenever we reject a value as too big, we shift it one place to the right.

Now, think about it. When we find the first item that is equal to or less than the new value, we have what we want: a value that should be to the left of our new value in the final list, and, to the right of it, an empty slot (remember, we've been moving every value that we pass). To cap it off, the value to the right of the empty slot is a value that we've already rejected - meaning it's a value that should be to the right of the new element in the final list! Simply insert the new element into the empty slot, and we have completed the insertion step.

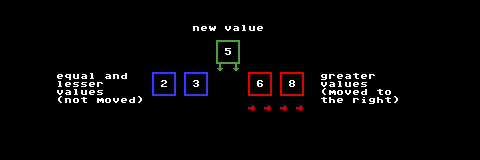
Let's implement the insertion step in C.

#include <stdio.h>

int main() {
    long sorted_section[4] = { 2, 5, 7 };
    long key = 4;
    // key is the value we want to insert
    int j = 2;
    // j is the index we are checking
    // it starts at 2 because that's 
    // the last index in the array
    while (j >= 0 && sorted_section[j] > key) {
        // until we find an equal or lesser value
        sorted_section[j + 1] = sorted_section[j];
        // move the current value to the right
        j--;
        // and move on to the next index 
    }
    sorted_section[j + 1] = key;
    // we found the first equal or lesser value
    // so put key in the empty spot to the right of it

    for (int i = 0; i < 4; i++) printf("%ld ", sorted_section[i]);
    // print the array

    return 0;
}

Let's run it.

• ./insertion_sort 2 4 5 7

Correct! Our new element was inserted in its correct place.

Once we understand how the insertion step works, we can implement the full algorithm, by just performing the insertion step on every element in the input array, one by one! I'll be using some utility functions I made for parsing command-line arguments into a long *.

#include "../clilonglist.h" 
// my command-line input utility functions
#include <stdlib.h>

long * insertion_sort(int inputc, long * inputv) {
    // inputc: the length of the input array
    // inputv: the input array itself
    
    long * outputv = malloc(sizeof(long) * inputc);
    // we will always keep this array sorted
    
    for (int i = 0; i < inputc; i++) {
        // for every value in the input
        long key = inputv[i];
        // grab the value and call it "key"
        int j = i - 1;
        // the index we are going to check first
        // it starts at i - 1 because that will
        // always be the last element in the 
        // sorted list
        
        // begin insertion step
        while (j >= 0 && outputv[j] > key) {
            outputv[j + 1] = outputv[j];
            j--;
        }
        outputv[j + 1] = key;
        // insertion step done!
        // key is now in its sorted
        // position in outputv
    }

    free(inputv);
    return outputv;
}

int main(int argc, char * argv[]) {

    int inputc = argc - 1;
    long * inputv = extract_long_list(inputc, argv);
    // use my utility functions to grab the 
    // command line arguments as an array of longs

    inputv = insertion_sort(inputc, inputv);

    print_long_list(inputc, inputv);

    free(inputv);
}

Looks good. Let's run it.

• ./insertion_sort -5 7736 8 23 4 0 -5 0 4 8 23 7736

As expected, it sorts the list!

Sorting in place

There's one more improvement we can make, though. We've been using separate output and input arrays - the sorted "left hand" and the unsorted "right hand" - but we don't strictly need to. Think about it. If we have one stack of cards in each hand, what prevents us from just connecting them and treating them as two subsections of the same stack? All we need to do is remember what part of the array is the "left hand", and which is the "right." Fortunately, we do know this! We always know how long the sorted section is, because we made it ourselves!

Our algorithm actually has everything it needs to sort the input array in place. All we have to do is swap some names:

#include "../clilonglist.h" 
// my command-line input utility functions
#include <stdlib.h>

long * insertion_sort(int inputc, long * inputv) {
    // inputc: the length of the input array
    // inputv: the input array itself
    
    for (int i = 0; i < inputc; i++) {
        long key = inputv[i];
        int j = i - 1;
        
        // begin insertion step
        while (j >= 0 && inputv[j] > key) {
            inputv[j + 1] = inputv[j];
            j--;
        }
        inputv[j + 1] = key;
        // insertion step done!
    }

    return inputv;
}

int main(int argc, char * argv[]) {

    int inputc = argc - 1;
    long * inputv = extract_long_list(inputc, argv);

    inputv = insertion_sort(inputc, inputv);

    print_long_list(inputc, inputv);

    free(inputv);
}

And it still works exactly the same!

• ./insertion_sort -5 7736 8 23 4 0 -5 0 4 8 23 7736

Conclusion

You might be wondering how we perform this operation on only one list without accidentally overwriting any values in the unsorted section. Fortunately, the way this algorithm works guarantees that unsorted values will never be touched by side effects of the insertion step! Put some cards on a table and try it for yourself.